In questa pagina analizzeremo il fenomeno fisico relativo alla stabilità traversale del sommergibile, ovvero la sua capacità di ritornare in equilibrio dritto, dopo essere stato soggetto ad uno sbandamento (ossia ad una rotazione attorno al suo asse longitudinale), a seguito dell'applicazione di una forza esterna che causa una perturbazione dell'equilibrio iniziale.
Il fenomeno sussiste sia per i battelli completamente immersi che per quelli in emersione, tuttavia lo stesso assume formulazioni diverse nei due casi. Per questo motivo li studieremo in maniera separata.
1. Battello immerso
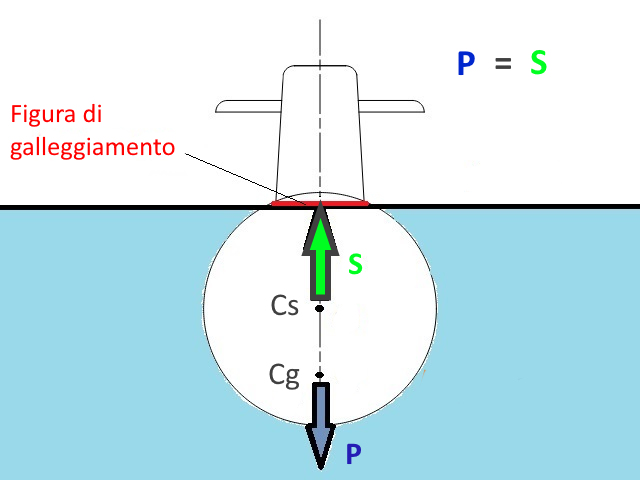
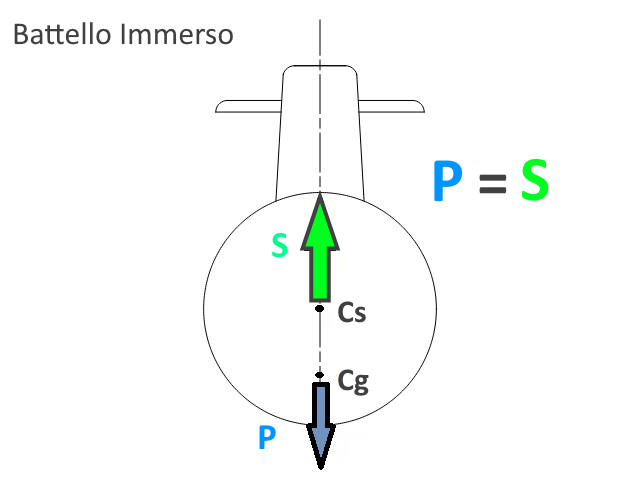
Consideriamo un battello immerso in una condizione di equilibrio stabile dritto (battello perfettamente dosato, P=S, e in assetto completo). Il Centro di spinta Cs e il Centro di gravità Cg saranno perfettamente allineati (sull'asse verticale passante per Cs) e su di loro agiscono il peso P e la spinta S (forze uguali e contrarie). In questa configurazione, il Cs è anche il centro geometrico dello scafo e quindi su di lui passerà anche l'asse longitudinale del battello.
In questa condizione, il peso P del battello corrisponde al suo Dislocamento in immersione ∆i; sussistendo l'equilibrio, il Dislocamento sarà uguale alla forza della Spinta idrostatica S (generata per il Principio di Archimede).
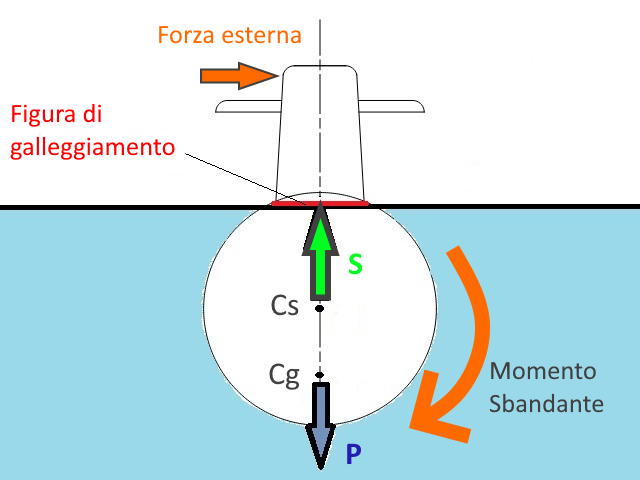
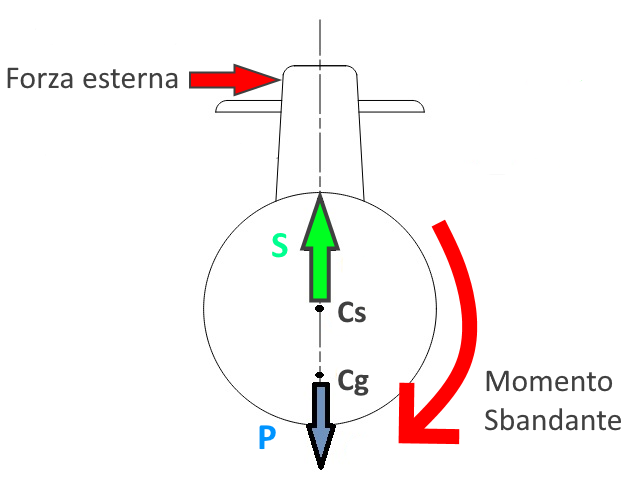
Supponiamo ora di perturbare l'equilibrio sopra descritto applicando una forza esterna che tenda ad inclinare lateralmente (sbandare) il battello, facendolo ruotare lungo il suo asse longitudinale.
Osservando il fenomeno sul piano trasverale, la forza esterna applicata ad una certa distanza dal Centro di spinta (che è il centro di rotazione dello scafo) crereà un momento sbandante (in questo caso diretto in senso orario). Tale momento causerà una rotazione del battello attorno al Cs.
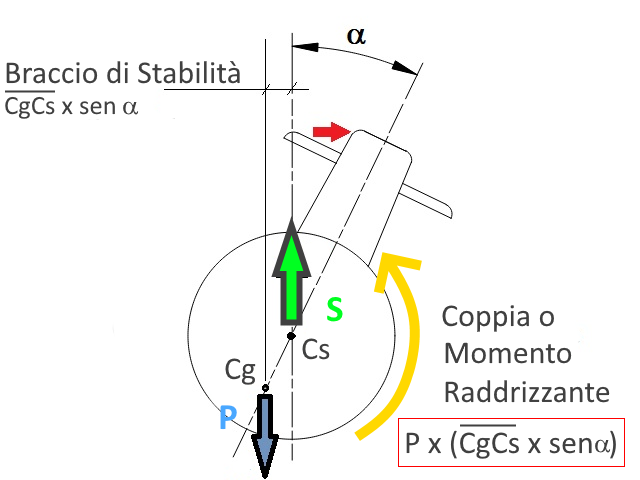
Supponiamo che il battello sia ruotato di α gradi. Il Cs è rimasto nella sua posizione e su di lui continua ad agire la spinta S; Cg si è invece spostato e con lui si è anche spostato il punto di applicazione della forza peso.
In tale condizione, la forza P e la forza S costituiscono una Coppia di forze uguali e contrarie che genera un momento raddrizzante che va ad opporsi al momento sbandante generato dalla forza esterna.
Nel momento in cui eliminiamo la forza esterna, il momento raddrizzante farà ruotare il battello (questa volta in senso antiorario) fino a raggiungere nuovamente la condizione di equilibrio iniziale.
Dal punto di vista numerico possiamo dire che l'intensità del momento raddrizzante è pari alla forza peso P moltiplicata per il braccio di stabilità (che rappresenta la distanza minima tra le due rette parallele su cui agiscono le forze P e S). Facendo ricorso alla trigonometria possiamo dire che tale braccio è pari alla lunghezza del segmento CsCg moltiplicato per il seno dell'angolo α.
Il momento raddrizzante sopra descritto, che si genera quando incliniamo il battello di un angolo α si chiama Momento di Stabilità Trasversale e lo indicheremo con Mst (α). Esso sarà quindi :
Mst (α) = P x CgCs x sen α
In architettura navale si usa indicare la lunghezza del segmento CgCs con "a", così come si usa il concetto di dislocamento Δ per indicare il peso P (nel nostro caso è il dislocamento immerso Δi). Per quanto sopra la formula diventa:
Mst (α) = Δi x a x sen α
Da questa formula possiamo dedurre alcune importanti considerazioni:
Il momento di stabilità sarà maggiore quanto maggiori saranno il dislocamento e l'angolo di sbandamento (e questo è abbastanza ovvio);
il momento di stabilità aumenta anche all'aumentare di a (ossia della distanza tra Cg e Cs). Considerando che la posizione di Cs è praticamente immutabile (dipende dalle forme geometriche dello scafo), possiamo dire che la stabilità dipende moltissimo dalla posizione di Cg (che è variabile e dipende dal posizionamento dei pesi a bordo). Più basso è il Centro di Gravità e migliore sarà la stabilità !! Questo spiega la necessità di mantenere quanto più possibile i pesi di bordo in posizione bassa (vecchia regola nota a tutti i marinai).
Su un battello di medie dimesioni (Δi = 1500 ton) il valore di a è di circa 2 metri.

2. Battello emerso
Consideriamo un battello in superficie nella solita condizione di equilibrio stabile dritto (battello perfettamente dosato, P=S, e in assetto completo). Il Centro di spinta Cs e il Centro di gravità Cg saranno perfettamente allineati (sull'asse verticale passante per Cs) e su di loro agiscono il peso P e la spinta S (forze uguali e contrarie).
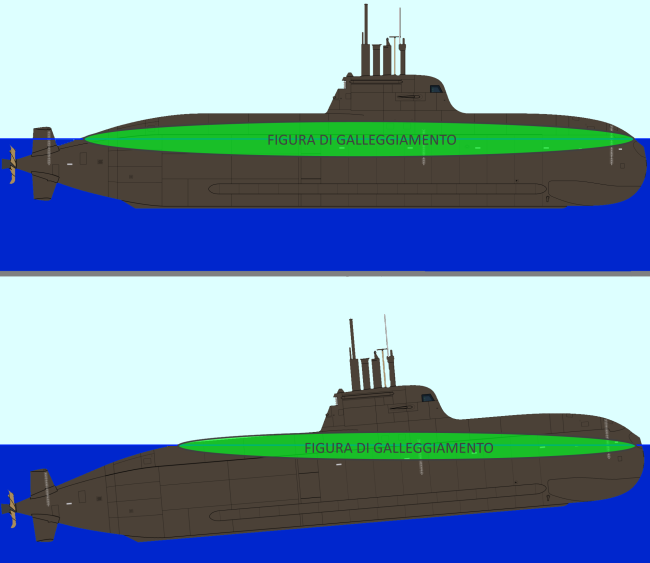
A differenza del caso precedente (battello immerso) notiamo che il Cs non è più il centro geometrico dello scafo immerso (in quanto una parte dello scafo è fuori dall'acqua e non concorre quindi alla forza di spinta di Archimede). In questa condizione di galleggiamente notiamo anche la presenza di una Figura di galleggiamento, che viene definita come l'area piana (orizzontale) ottenuta dall'intersezione tra lo scafo e la superficie del mare. Come vedremo, la forma e le dimesioni della figura di galleggiamento costituiscono un fattore molto importante nell'architettura navale.
Supponiamo ora di perturbare l'equilibrio sopra descritto applicando una forza esterna che tenda ad inclinare trasversalmente (sbandare) il battello, facendolo ruotare lungo il suo asse longitudinale.
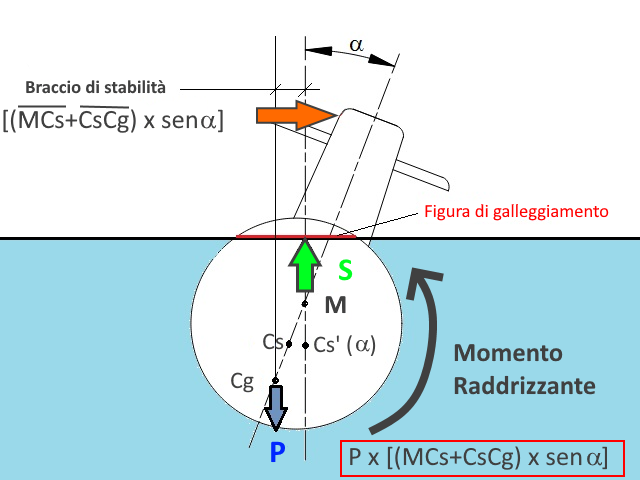
La forza esterna applicata crereà un momento sbandante (in questo caso diretto in senso orario) che causerà una rotazione del battello. Ma - attenzione - in questo caso (emersione) la rotazione non avverrà più attorno al Cs, in quanto il battello ruoterà attorno ad un altro punto che convenzionalmente viene chiamato Metacentro Trasversale Iniziale e indicato con "M".
Il battello è ruotato di α gradi attorno al metacentro M e su quest'ultimo, in questo caso, agisce la forza di spinta S. Il Cs si è spostato in una nuova posizione che chiameremo Cs'(α). Anche Cg si è postato e con lui si è anche spostato il punto di applicazione della forza peso P.
Quanto sopra viene dall'Architettura Navale a seguito di dimostrazioni piuttosto complesse che non tratterò in questa sede. E' tuttavia importante sapere che la posizone del metacentro M dipende esclusivamente dalla dimensione e dalla geometria della Figura di galleggiamento.
Anche in questo caso, la forza P e la forza S costituiscono una Coppia di forze uguali e contrarie che genera un momento raddrizzante che va ad opporsi al momento sbandante generato dalla forza esterna.
Nel momento in cui eliminiamo la forza esterna, il momento raddrizzante farà ruotare il battello (questa volta in senso antiorario) fino a raggiungere nuovamente la condizione di equilibrio iniziale.
Dal punto di vista numerico possiamo dire che l'intensità del momento raddrizzante è pari alla forza peso P moltiplicata per il braccio di stabilità (che rappresenta la distanza minima tra le due rette parallele su cui agiscono le forze P e S). Facendo ricorso alla trigonometria possiamo dire che tale braccio è pari alla lunghezza del segmento MCg moltiplicato per il seno dell'angolo α.
Il momento raddrizzante sopra descritto, che si genera quando incliniamo il battello di un angolo α si chiama Momento di Stabilità Trasversale e lo indicheremo con Mst (α). Esso sarà quindi :
Mst (α) = P x MCg x sen α
ovvero
Mst (α) = P x (MCs + CsCg) x sen α
In architettura navale si usa indicare la lunghezza del segmento CgCs con "a", e del segmento MCs con "r" che viene denominato come Raggio Metacentrico Trasversale Iniziale. Continuando ad usare il concetto di dislocamento Δ per indicare il peso P (nel nostro caso è il dislocamento in superficie Δs), la formula diventa:
Mst (α) = Δs x (r + a) x sen α
Da questa formula possiamo dedurre alcune importanti considerazioni:
Il momento di stabilità sarà maggiore quanto maggiori saranno il dislocamento e l'angolo di sbandamento (e questo è abbastanza ovvio);
il momento di stabilità aumenta all'aumentare di a (ossia della distanza tra Cg e Cs). Considerando che la posizione di Cs è praticamente immutabile (dipende dalle forme geometriche dello scafo), possiamo dire che la stabilità dipende moltissimo dalla posizione di Cg (che è variabile e dipende dal posizionamento dei pesi a bordo). Più basso è il Centro di Gravità e migliore sarà la stabilità !! Questo spiega la necessità di mantenere quanto più possibile i pesi di bordo in posizione bassa (vecchia regola nota a tutti i marinai).
il momento di stabilità aumenta anche all'aumentare di r che, a sua volta, cresce con l'aumentare della superficie della Figura di galleggiamento (anche se, come abbiamo già detto, r dipende anche dalla forma della Figura di galleggiamento e quindi non solo dalle sue dimesioni).
Se non c'è figura di galleggiamento (immersione) allora r è nullo !
La formula di cui sopra può anche essere espressa con:
Mst (α) = (Δs x r x sen α) + (Δs x a x sen α)
Considerando che r dipende solo dalla forma dello scafo e della sua figura di galleggiamento, e che a dipende solo dai pesi e dalla loro disposizione a bordo, si usa nominare i due fattori della formula precendente in:
Fattore di forma: Δs x r x sen α
Fattore di peso: Δs x a x sen α
Quanto sopra intruduce il concetto di stabilità di peso e di stabilità di forma che, insieme, caratterizzano la stabilità di un sommergibile (e anche delle navi di superficie, anche se in modo molto diverso).
3. Conclusioni
Possiamo dire, in generale, che la stabilità di un sommergibile è caratterizzata da un Momento di stabilità trasversale Mst che, in presenza di un angolo di sbadamento α, è sempre individuabile con la formula:
Mst (α) = Δ x (r + a) x sen α
( tenendo a mente che in immersione r = 0 ).